반응형
LIFT evening Seoul을 다녀왔습니다.
LIFT는 사회 안에서 기술의 도전과 기회에 대한 콘퍼런스입니다. 스위스 제네바에서 LIFT 06과 LIFT 07 행사가 열린적이 있죠. 더 자세한 사항을 알고 싶으시다면 LIFT conference 공식 홈페이지를 방문하세요.

사용자 삽입 이미지

LIFT korea


2007년 9월 12일에 열렸던 LIFT evening Seoul은 2008년 6월에 예정된 LIFT Asia의 예비 행사라고 생각하면 될 듯 합니다. 물론 스위스 제네바에서 열리던 LIFT 08 행사는 2008년 2월에 열립니다. 예비 행사라서 그런지 발표자 분들이 원래 이렇게 짧은시간에 맞춘 내용이 아니라서(원래는 LIFT 07에서 더 충분한 시간으로 발표되었던 내용으로 보입니다.) 그런지 발표하실 때 압축해서 발표를 하신다는 느낌이 들었습니다.

압구정역에서 내려서 유림아트홀을 찾는데 길이 복잡해서 헤매다가, 어떤 여성 분이 유림아트홀을 찾아 내셔서 시작하기 전에 무사히 들어갈 수 있었습니다. 이미 자리 앞에는 많은 분들이 오셔서 이야기를 하고 계셨는데, 외국 분들이 많이 보이셔서 분위기가 익숙하지 않았습니다.

첫 번째 발표는 Adam Greenfield 씨가 도시에 관한 주제로 발표해주셨습니다. 영어로 발표가 진행되었지만, 다행히도 동시통역이 제공되어서 잘 들을 수 있었습니다. "도시학"이라는 학문이 있다는 걸 그때 처음 알았습니다. 도시가 점점 즐거움은 사라지고, 더럽고, 미끄러우며, 미관이 악화되는 방향으로 변하는 현 상황을 제시하면서, 더 나은 방향으로 나아갈 필요가 있다고 했습니다. 우리나라도 버스나 지하철을 타다보면 귀에 이어폰을 끼고 음악을 듣거나, DMB로 TV를 보거나 하는 모습 등을 자주 볼 수 있는데, 이런 현상은 미국에서도 있다고 합니다. Adam Greenfield 씨는 이런 현상을 사람들이 System에 참여하기를 그만두는 현상으로 분석했습니다.

이에 대해 더 관심이 있으시다면 Adam Greenfield 씨가 쓰신 Everyware라는 책을 보시는 것도 좋을 듯 합니다.

뒷 부분은 잘 알아듣지는 못했는데, Nike+iPod, bio-medical(PET), 휴대전화로 이용하는 지리정보시스템, 인식거리 넓은 RFID[각주:1] 등의 이야기가 나오면서, 행동(또는 패턴/시각화)으로 문제를 해소해야 한다는 이야기가 나온 것으로 기억합니다.

이런 시스템에도 단점은 있기 마련인데, 지나치게 좋은 가독성이라는 것입니다. 자기가 받아들일 수 있는 정보량보다 너무 많은 정보가 주어져서, 사람에게 안 좋을 수 있다는 이야기로 들렸습니다.

두 번째 발표는 Bruce Sterling 씨가 해주셨습니다. 미래에 의자를 매개로 한 이야기를 애니메이션으로 보여주고, 이를 뒤에서 분석하는 식으로 발표가 진행되었습니다. 의자 이야기의 줄거리는 다음과 같습니다.

남자와 여자가 자기가 원하는 스타일의 의자를 온라인 상에서 주문합니다. 주문을 받은 회사는 넓고 적당히 얇은 판에 도면을 인쇄해서 잘라 조립합니다. 조립된 의자는 남자와 여자에게 배달됩니다. 그 의자는 RFID 기능 등 다른 기능들도 포함되어 있습니다. 어느날 그 의자를 옥상에 두었다가 그 의자에 벼락이 치게되어 망가지게 됩니다. 그런데 의자를 주문했던 회사에서 신 모델 의자를 새로 주겠다고 합니다. 그러면서 회사 사람이 망가진 의자를 수거해가고, 그 의자를 의자재료로 쓰이는 넓은 판으로 재활용하기 위해 가루로 만듭니다.
세 번째 발표는 XL Games의 송재경 씨가 해 주셨습니다. 온라인 게임의 변화를 몇 단계로 나누어 짚어 주셨는데요. MUD 게임에 대한 이야기가 나왔습니다. 플레이 해 본 경험은 없는데, 공간적 감각에 결함이 있는 경우가 있다고 합니다.
일반적인 2D 게임에서 아래로 한칸, 옆으로 두칸 움직이고, 위로 한칸 움직이면 처음 출발했던 위치와는 달라야 합니다. 그런데 머드 게임에서는 위와 같이 움직일 경우 처음 위치로 돌아오게 됩니다.
2D MMORPG로 넘어오면서 지리적으로 올바른 형태가 되고, 교통수단(말, 배 등)이 등장했습니다. 사람의 키를 기준으로 해서 한 세계의 크기는 400 km2 정도 된다고 합니다. 이보다 크면 이동하는 데 시간을 보내느라, 사용자가 피곤해지기 때문이죠.
이후 3D MMORPG에서는 던전에서도 병목현상(또는 악성사용자가 길을 막는 행위)을 막기 위해 즉석으로 생성되는 던전을 도입하게 됩니다.  이동 시간이 지나치게 많아 역효과를 주는 일을 막기 위해, 교통수단도 늘어나고요. 현실에서 썼던 상식이 가상공간에서도 통하도록 설계를 하도록 한다고 합니다.
미래 MMORPG에 대해서도 조심스럽게 이야기해주셨는데요.
  • 지금의 세계보다 더 큰 세계가 도입될 것인가(병렬 연산등을 도입한 서버 퍼포먼스가 관건)
  • 손수제작물 열풍에 힘입어 사용자 주도의 공간이 도입될 것인가
  • 던전처럼 주택도 즉석으로 생성될 것인가(이를테면 아파트)
  • 사람과 사람 사이에 서로 통과할 수 없게 할 것인가(악용의 위험)
  • 환경변화를 도입할 것인가[각주:2]
  • 환경 변화의 도입이 비용 대비 얼마나 가치를 줄 것인가
  • 인위적 세계 바꾸기를 가능하게 할 것인가(파괴/건축, 세계가 황폐화 되는 건 아닐까)
등을 들을 수 있었습니다.

네 번째 발표에서는 건축가 유석연 씨가 '방'에 대한 자신의 연구와, 도시에 관한 자신의 여러 연구에 대해서 발표해 주셨습니다. 중간에 들었던 Glocal에 대한 이야기가 인상깊었습니다. 도시계획방법론 등에 대해서도, 배경지식이 부족해 충분히 이해하지는 못했지만 흥미로워 보였습니다. 특히 노드와 그래프로 이루어진 다이어그램을 보면서, 물리와도 상성이 잘 맞겠다는 생각이 들었습니다.

사용자 삽입 이미지

아사히맥주 레스토랑 사진


발표 이후에는 유림아트홀에서 1분 거리인 아사히맥주에서 뒷풀이가 있었습니다. 분위기가 상당히 자유롭고 수평적인 느낌이 들더군요. 안주는 낯설었지만, 맥주도 맛있었고요. 여러 사람들과도 만나서 조언도 듣고, 이야기도 나누어 보고 할 수 있어서 보람을 느꼈습니다. 외국 분들이 많아서 새삼스럽게 "영어가 중요하다."라는 사실을 느끼게 되더군요.
  1. 이 부분은 홍콩의 교통카드 예를 들면서, 핸드백안에 교통카드를 넣고 개찰구를 그냥 통과만 해도 지불이 된다고 하더군요. 우리나라의 경우에는 교통카드를 인식기기에 5cm 내외로 대야하는 것과 대비되더라고요. [본문으로]
  2. 마비노기에서는 낮과 밤이 변하고, 비가 오는 날, 번개가 치는 날, 맑은 날이 있다. [본문으로]
반응형
반응형
익스트림 프로그래밍(Extreme Programing Explained 2/E)를 읽었습니다. Extreme Programming, 줄여서 XP는 "애자일 소프트웨어 개발"에서 논의되는 방법론 중의 하나입니다. 한국 eXtreme Programming 사용자 모임도 있고요.
첫 부분에 XP에 대한 설명과 1부 XP 탐험하기에 대해서는 차근차근 XP가 추구하는 가치, XP의 실천방법 등에 대해 나와 있습니다.

제일 관심있게 읽었던 부분은 "제약이론"입니다. 세탁하는 과정을 비유로 들어서 제약 이론을 설명하고 있었는데, 제약 지점을 찾는 것에 대한 이야기를 하고 있었습니다. 제약 이론은 전체적인 처리 역량을 좋게하는데 초점을 두고 있다는 점에서 좋은 방법으로 보입니다. 다만 XP를 적용함으로써 새로운 제약지점 부서는 주목받는 일을 원하지 않기 때문에, XP가 도입되기 여렵다고 하는 점에서 아쉬웠습니다.

도요타 생산 시스템이 언급되는 장도 있었습니다. 이 장에서 언급되었던 Lean Software Development가 2007년 9월 중순에 번역본으로 나왔던 소식을 들었던 터라, 반가웠습니다. 테일러주의가 보편적으로 사회에 자리잡기는 했지만, 특정 분야(이를테면 소프트웨어 개발)에서는 그에 적합한 방법을 사용하는 것이 맞다고 봅니다.

책 끝부분에 많은 참고문헌이 소개되어 있어서,
어떤 주제에 대해 관심이 있다면 찾아서 학습할 수 있도록 돕고 있습니다.

블로그에 읽었던 책을 틈틈이 정리하고는 하는데, 이번주는 정말 책을 열심히 읽었네요.
익스트림 프로그래밍(Extreme Programming) 상세보기
켄트 벡 지음 | 인사이트 펴냄
익스트림 프로그래밍 입문서 개정2판. 이 책은 XP의 소개와 운전하는 법 배우기, 가치와 원칙, 실천 방법, 제약 이론, XP확장, XP의 철학 등의 내용을 담았다. 저자는 이 책에서 소프트웨어를 개발하는 데 필요한 핵심과 실천 방법들을 소개하고, 프로젝트를 어떻게 더 잘 운영할 것인지, 사실에 기반을 둔 계획성들에 관하여 이야기한다. 《익스트림 프로그래밍》에서는 XP를 적용하여 얻게 되는 가치와 조화되는 삶에 관한 실천

반응형
반응형
맨먼스 미신을 도서관에서 빌려 읽었습니다. The Mythical Man-Month라는 책을 여러 책에서 추천하고 있었는데, 번역본이 출간되어 반가웠습니다. 책 겉면에는 출간 20주년 기념판이라고 써 있었는데, 본래 책이 1995년에 나왔으니 32년 넘게 시간이 흘렀군요. 꾸준하게 다양한 배경의 사람들이 읽었다고 들은 책이라 기대가 되었습니다. "소프트웨어 컨플릭트 2.0"처럼 한겨레신문에서 제공하던 서체를 사용하던데, 처음에는 좀 어색했지만 적응하고 나니 글씨도 큼직하고 읽기 좋습니다.

이 책의 구조에서 가장 깊은 인상을 남긴 것은 각 장이 시작될 때마다 한 페이지 전체에 관련된 그림이나 사진이 실리는 모습이었습니다. 앞의 그림을 떠올리면서 책을 읽어나가다보면, "이런 주제를 드러내려고 이런 그림을 실었구나!"하고 느낄 수 있었습니다.

다른 소프트웨어 공학 에세이에서도 빈번하게 나타나는 주제인, "은총알(Silver bullet)"에 대한 언급도 있었습니다(은총알은 없다). 소프트웨어 공학에서 발생하는 괴물같은 주제를 늑대인간에 비유하고, 이른 해결할 돌파구를 늑대인간을 무찌를 수 있다고 알려진 은총알에 비유한 것인데요. 흥미롭게 읽었습니다.

다른 한 가지는 프로젝트 팀을 수술 팀이라는 은유로 생각했던 부분이었습니다. 이 해결책은 Harlan Mills라는 분이 제안했던 것인데, 문제를 조각내지 않고 많은 손이 필요한 부분에 적절히 역할을 맡아 효과적인 문제 해결을 위해 노력한다는 점이 마음에 들었습니다.

맨먼스 미신의 초판에서 제안되었던 사항들이 지금은 어떻게 되었는지, 맨먼스 미신의 초판에 대한 저자의 고찰과 회고가 담긴 장들이 뒷부분에 추가되어 있었습니다. 과거가 미래 예측에 도움이 되는가에 대해서는 논란이 있지만, 그래도 현재 살아가는데 과거의 지식이 가치있으리라고 생각합니다. 책에 나온 기술들이 현재 사용되는 것과 다소 동떨어질 수 있지만, 근본적인 가치는 크게 변하지 않아서 여러 사람들에게 도움이 되리라 생각합니다.
맨먼스 미신 상세보기
프레더릭 브룩스 지음 | 케이앤피북스 펴냄
컴퓨터 공학 이론서. 이 책은 대형 프로그래밍 프로젝트에서 소형 프로그래밍 프로젝트와 다른 종류의 관리 어려움을 극복하는 방법을 설명하고 소프트웨어 공학 관리의 특징에 관하여 에세이 형식으로 구성했다.
반응형
반응형
애자일 프랙티스를 읽었습니다. Practices of an Agile Developer의 제목 공모 이벤트에 참여만 했을 뿐인데 책을 받게 되어 기쁩니다. 책을 처음 펼치자 마자 맞닥뜨린 인용구가 인상적이었습니다. 책에서는 한 장이 시작할 때마다 그와 관련된 속담, 격언, 인용구 등으로 주제를 도입하고 있습니다. The Pragmatic Programmer(실용주의 프로그래머로 국내에서 번역되었죠.)의 공동저자 중 한 사람인 앤디 헌트와 Agile Developer의 설립자 벤캣 수브라마니암이 쓴 이 책은 말 그대로 적용 가능한 실천 지침들을 제공하고 있습니다.

1장에서는 우선 애자일 소프트웨어 개발에 대한 배경적 지식을 논합니다. 2장부터 8장까지 각 장의 서두에는 어떤 지침들이 나올 예정인지 간략히 소개되어 있습니다. 각 지침의 첫 부분에는 악마가 사람들이 피해야 할 나쁜 습관을 일러줍니다. 지침에 관련된 에피소드나 실례를 제시하여 이 지침이 왜 유용한지 거부감없이 느낄 수 있게 하며, 천사가 사람들이 가져야 할 좋은 습관을 일러 줍니다. 책 표지에 악마와 천사가 등장하는 것은, 독특한 캐릭터들이 지침의 설명 부분에 등장하기 때문으로 생각합니다. 그 후에는 "어떻게 느껴야 하는가?"라는 부분이 있습니다. 말 그대로 이런 느낌을 갖고 있다면, 바르게 가고 있다는 안내를 해 주기 위해 도입된 것으로 보입니다.

하지만 어떤 지침이든 지나치게 적용하거나, 느슨하게 적용하면 그 효과를 제대로 발휘하지 못할 수 있습니다. 이런 부분을 바로잡기 위해 "균형 유지하기"에서는 어떤 부분에 중점을 두어야 하고, 어느 정도가 적당한지 지적합니다.

에필로그를 읽다보니 전에 보았던 Ship It!을 개발 기반의 마련을 위한 Starter Kit으로 추천하더군요. 뒤에는 여러 참조 링크와 관련 문헌들이 소개되어 있고, 실용주의 프로그래머처럼 가이드라인 요약본이 뒷표지 앞에 붙어 있습니다.

최근에 IT 회사에 다니시는 분에게 이야기를 들을 기회가 있었습니다. 그 분이 의아해하셨던 것은, "왜 대학에서는 테스트를 가르치는 과목이 없느냐?"였습니다. 애자일의 인프라스트럭처에는 "유닛테스트"가 중요한 위치를 차지하고 있습니다. "테스트 주도 개발"이라는 움직임이 보이고, 국제 테스팅 컨퍼런스(2007년 10월 초에 서울 코엑스에서 열린다고 합니다.) 도 열리고 있으며, 수습 불가능한 스파게티 코드가 되는 일을 피하고 유지보수를 쉽게 하기 위해서라도 테스트의 중요성은 날로 커지고 있습니다. 그래서, 테스트에 대한 과목도 교과과정에 들어있으면 하는 바람이 생겼습니다.

애자일이라는 걸 머리로는 알고 있지만, 어떻게 실천해야 하는가에 대해 막막함을 느낀 분들도 있을거라 생각합니다. 이 책에서 시도하기 쉬운 지침을 선택하여 점진적으로 적용한다면, 개인과 팀에 긍정적인 변화가 생기지 않을까 생각해 봅니다.
애자일 프랙티스 상세보기
벤캣 수브라마니암 지음 | 인사이트 펴냄
애자일 소프트웨어 개발 전문서. 이 책은 45개의 애자일 프랙티스 사례를 통해 어떤 문제에프랙티스를 적용하고 맞추는 방법을 통해 애자일 소프트웨어를 익힐 수 있도록 구성했다. 프랙티스를 올바르게 적용했을 때 어떻게 느껴지는지, 과하게 적용하는 것과 성기게 적용하는 것 사이에서 균형을 맞추는 방법을 설명하고 코딩과 디버깅에 관한 내용도 함께 설명한다. 책 뒤편에는 애자일 프랙티스 자료에 관한 내용도 포함했다.
반응형
반응형

한국 루비 사용자 포럼
BarCamp RubykrSeminar4
루비 세미나 공식 블로그

사용자 삽입 이미지

4회 루비 세미나


2007년 9월 8일.

4회 루비kr세미나에 다녀왔습니다. 장소는 3호선 양재역 근처의 다음커뮤니케이션 건물 3층이었습니다. 전에 매쉬업 세미나때문에 갔던 곳이라 길이 익숙했습니다. 원래 2시부터 시작이었는데, 일찍 왔는데 문이 잠겨있길래 문 앞에서 기다리고 있다가 직원 분이 카드로 문을 열어주셔서 들어갈 수 있었습니다. 엘리베이터에도 카드를 찍으시던데 정말 신기하더군요.

저녁의 다른 약속과 겹쳐서 아쉽게도 세션을 다 들을 수는 없었습니다. 세션 1에서는 코디안님이 Rails 기반의 RSS 서비스를 소개하셨습니다. Main DB를 사용하지 않고 API만으로 RSS 리더를 구현하는 모습이 신기했습니다. 그 뒤에 나루라는 블로그 검색엔진과 관련있는 온네트에서 API에 대한 소개를 해주셨는데요, 아직 공중에 공개되지는 않았지만 그렇게 될 예정이라고 합니다.

세션 2에서는 우선 강규영님이 JSSpec을 이용한 JavaScript BDD(Behavior Driven Development) 개발을 주제로 발표해 주셨습니다. BDD는 TDD(Test Driven Development)에서 갈라져 나온 개발양식이라고 이해했는데, 맞는지 모르겠습니다. 끝에 TDD에 관한 바른 이해를 돕는 여러 좋은 말을 들었습니다. (테스트 주도 개발을 어쩌다가 읽고난 뒤 오래되서 기억이 가물가물하네요.)
그 다음에는 '쉽게 배우는 JRuby on Rails'를 번역하신 이창신님이 저자직강으로 JRuby에 대해 이야기해주셨습니다. 현재 C/C++나 Java가 꽤 많이 쓰이고 있는 것은 사실이고, 그래서 Java와 연동이되는 JRuby on Rails는 미래지향적인 곳이라면 한번 도입해보는게 좋다고 들었습니다. JRuby on Rails는 앞으로 Java SE 5를 선행 요구사항으로 하여 개발될 예정이라고 합니다.

세션 3에서는 RubyCocoa에 대해서 Jenix님이 발표해주셨습니다. 코코아 프로그래밍이라는 책을 번역하셔서 곧 나올 예정이라고 하셨는데 9월 15일에 정식으로 인사이트에서 출판되었군요. 맥 개발환경이 낯설긴 했지만, 드래그앤 드롭으로 버튼을 만들고 하는 모습이 신기해 보였습니다. 덧붙여 Objective-C에 대한 호기심도 생겼고요.

그 다음 부분부터는 듣지 못해서 아쉬움이 남았습니다. 일찍 나와서 루비가 신입 참가자에게 준다는 루비가 그려진 가방도 못받고, 기념품도 못 받은채 갔네요. 루비 세미나 공식 블로그를 방문하시면 4회 세미나의 내용을 동영상으로 보실 수 있습니다. 저도 시간나면 세션 3 뒷부분과 세션 4 부분을 봐야겠네요.

여러 유익한 점들을 배울 수 있어서 좋았습니다. 차회 세미나에 또 참가하고 싶네요.

반응형

반응형

Recapitulation

- Vector space V (to axioms)

- basis

- inner product <\vec{v},\vec{u}>

- dot product VV->k

-cross product VV->V

\vec{B} \times \vec{C} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ B_{x} & B_{y} & B_{z} \\ C_{x} & C_{y} & C_{z} \end{vmatrix} = \left | \vec{B} \right \vert \left | \vec{C} \right \vert \sin \theta_{k} \hat{n}

 dt \begin{pmatrix} a & b \\ c & d \end{pmatrix} =ad-bc
dt \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} =aei+dhc+bfy-(ceg+bdi+hfa)

diagonal하게 생각하면, 기억하기 쉽다.

geometrical meaning of \vec{B} \times \vec{C}

벡터 B가 x축 위에 누워있고, 벡터 C가 xy평면의 1사분면 중 어느 점을 가리키고 있는 상황이다.
벡터 B와 벡터 C 사이의 각은 θBC이다.

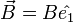
\vec{B}=B \hat{e_{1}} \vec{C}=C \cos \theta_{BC} \hat{e_{1}} + C \sin \theta_{BC} \hat{e_{2}} \Rightarrow \vec{B} \times \vec{C} = BC \cos \theta_{BC} \hat{e_{1}} \times \hat{e_{1}} + BC \sin \theta_{BC} \hat{e_{1}} \times \hat{e_{2}} =BC \sin \theta_{BC} \hat{e_{3}}

 \hat{e_{1}} \times \hat{e_{1}} = \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{vmatrix} =0

\hat{e_{1}} \times \hat{e_{2}} = \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} = \hat{e_{3}}

\hat{e_{1}} \times \hat{e_{2}} = \hat{e_{3}}; \hat{e_{2}} \times \hat{e_{3}} = -\hat{e_{1}}; \hat{e_{3}} \times \hat{e_{1}} = \hat{e_{2}} \hat{e_{2}} \times \hat{e_{1}} = -\hat{e_{3}}; \hat{e_{3}} \times \hat{e_{2}} = -\hat{e_{1}}; \hat{e_{3}} \times \hat{e_{1}} = -\hat{e_{2}}

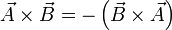
\vec{A} \times \vec{B} = - \left( \vec{B} \times \vec{A} \right) 

순서를 바꾸면 negation이 되는 이유

\begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{vmatrix}


triple scalar product

\vec{A} \cdot \left( \vec{B} \times \vec{C} \right)

\left | \vec{A} \right \vert \underbrace{\left | \vec{B} \right \vert \left | \vec{C} \right \vert \sin \theta_{BC}}_{area} \cos \beta

geometrical meaning: volume of pipe


triple cross product

\vec{A} \times \left( \vec{B} \times \vec{C} \right) \ne \left( \vec{A} \times \vec{B} \right) \times \vec{C} VVV->V \vec{A} \times \left( \vec{B} \times \vec{C} \right) = -\vec{C} \times \left( \vec{A} \times \vec{B} \right) = \vec{C} \times \left( \vec{B} \times \vec{A} \right) \vec{A} \times \left( \vec{B} \times \vec{C} \right) = \vec{B} \left( \vec{A} \cdot \vec{C} \right) -\vec{C} \left( \vec{A} - \vec{B} \right)

Levi-civita symbol

εijk

http://en.wikipedia.org/wiki/Levi-Civita_symbol

ε123 = ε231 = ε312 = 1 ε132 = ε213 = ε321 = − 1

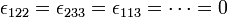
나란히 있는 두 숫자의 순서가 바뀌면 1의 부호가 바뀐다라고 생각하면 쉬움. \epsilon_{122}=\epsilon_{233}=\epsilon_{113}= \cdots =0

같은 숫자가 두개 있으면 0이라고 생각하기.

& Any permutations of two indices will introduce "-" sign


Usefulness of εijk

\hat{e_{i}} \times \hat{e_{j}} = \sum_{k} \epsilon_{ijk} \hat{e_{k}} where i,j,k=1,2,3

eg.

\hat{e_{1}} \times \hat{e_{2}} = \sum_{k} \epsilon_{12k}\hat{e_{k}}=\underbrace{\epsilon_{123}}_{1}

Another useful symbol: Kronedeker delta


http://en.wikipedia.org/wiki/Kronecker_delta

http://mathworld.wolfram.com/KroneckerDelta.html

\delta_{ij} = \begin{cases} 0, & \mbox{if }i \ne j \\ 1, & \mbox{if }i=j \end{cases}

eg. (m & n are dummy indices)

\vec{B} \times \vec{C} = \left( \sum_{m=1}^{3} B_{m} \hat{e_{m}} \right) \times \left( \sum_{n=1}^{3} C_{n} \hat{e_{n}} \right)

 = \sum_{m, n} B_{m}C_{n} \underbrace{\left( \hat{e_{m}} \times \hat{e_{n}} \right)}_{\sum_{j} \epsilon_{mnj} \hat{e_{j}}}

=\sum_{m,n,j} B_{m}C_{n} \epsilon_{mnj} \hat{e_{j}}

jth component

∑ BmCnεmnj
m,n
∑ BmCnεmn1
m,n

= B2C3 − B3C2

\sum_{k=1}^{3} \epsilon_{mnk} \epsilon_{ijk} = \delta_{mi} \delta_{nj} - \delta_{mj} \delta_{ni}

∑ εmjkεnjk = 2δmn
j,k

\sum_{i,j,k} \epsilon_{ijk}^{2}=6


eg 2. (Einstein convention - sum을 나타내는 sigma 기호 생략)

\vec{A} \times \left( \vec{B} \times \vec{C} \right)

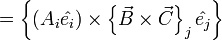
 = \left \{ \left( A_{i} \hat{e_{i}} \right) \times \left \{ \vec{B} \times \vec{C} \right \}_{j} \hat{e_{j}} \right \}

= A_{i} \underbrace{\left( \vec{B} \times \vec{C} \right)_{j}}_{B_{m}C_{n} \epsilon_{mnj}} \underbrace{\hat{e_{i}} \times \hat{e_{j}}}_{\sum_{k} \underbrace{\epsilon_{ijk}}_{-\epsilon_{ikj}} \hat{e_{k}}}

 =-A_{i}B_{m}C_{n} \underbrace{\epsilon_{mnj} \epsilon_{ikj}}_{\delta_{mi} \delta_{nk} - \delta_{mk} \delta_{ni}} \hat{e_{k}} 

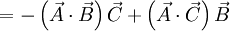
=-A_{i}B_{m}C_{n} \delta_{mi} \delta_{nk} \hat{e_{k}} + A_{i}B_{m}C_{n} \delta_{mk} \delta_{ni} \hat{e_{k}} =-A_{m}B_{m}C_{n} \delta_{nk} \hat{e_{k}} + A_{i}B_{k}C_{n} \delta_{ni} \hat{e_{k}} =-A_{m}B_{m}C_{n} \hat{e_{n}} + A_{n}B_{k}C_{n} \hat{e_{k}} =-\left( \vec{A} \cdot \vec{B} \right) \vec{C} + \left( \vec{A} \cdot \vec{C} \right) \vec{B}


gradient operator

\nabla \phi \left( x,y \right)

=\frac{\partial \phi}{\partial x} \hat{e_{x}} + \frac{\partial \phi}{\partial y} \hat{e_{y}}

d \phi \left( x,y \right) = \frac{\partial \phi}{\partial x} dx + \frac{\partial \phi}{\partial y} dy = \nabla \phi \cdot d \vec{r} -(1)

여기서 d \vec{r} = dx \hat{e_{x}} + dy \hat{e_{y}}

식 (1)이 최대가 되려면 \cos \theta \left | \nabla \phi \right \vert \left | d \vec{r} \right \vert 에서 maximum at θ = 0

θ는 d \vec{r} 벡터와 \nabla \phi 벡터 사이의 각

반응형
반응형

Q: What is a vector?



short answer: physical quantities that have a magnitude as well as a direction.
eg.
사용자 삽입 이미지

r, v, a in vector


exteded definition (answer): an element of a vector space.

Q: What is a vector space?


answer: a set whose elements are vectors that obey a certain set of rules.
1. If ,
2. If , then (c: constant)
3.
4. such that
5. such that
6.
7.
8.
9.
10.
eg 0.
eg 1.
cf.

eg 2. V: matrices

eg 3. Laplace equation (→ normal modes)

<basis> a set of linearly independent vectors that spans V. say
forms a basis for V


if and only if ai = 0
and (any vectors in V)

<inner product>

a mapping that maps two vectors to a scalar. < vi,vj >
1) < au1 + bu2,v > = a < u1,v > + b < u2,v > (a,b are constants)
2)
3) or 0 if and only if
eg 1. dot product



eg 2.


Dot product






Cross product



반응형
반응형
6. Gravitation and Central Forces (중력과 중심력)
지구에서 관측되는 별의 움직임이 서에서 동으로 갈 때 거꾸로 움직여서, 고리를 그리는 현상이 발견됨.
Ptolemy: epicycle(주전원, 그 중심이 다른 큰 원의 툴레 위를 회전하는 작은 원)을 주장.
코페르니쿠스: 지동설 주장.
Johannes Kepler: Tycho Brahe의 데이터를 갖고 세 법칙을 발견함.
1. 타원궤도
2. 면적속도 일정
3. 주기 T의 제곱은 장축의 세제곱에 비례
갈릴레오 갈릴레이:
Isaac Newton: Universal gravitation(만유인력)
Newton의 3개 운동법칙 - 관성, F=ma, 작용-반작용
사용자 삽입 이미지

formula of universal gravitation


F의 앞 첨자는 힘을 경험하는 곳, 뒤 첨자는 힘의 source이다.
위에서 r 벡터는 i에서 j로 향하는 위치벡터.
만유인력 상수
사용자 삽입 이미지

gravitational constant


반응형
반응형
PDG에서 온 소포 이후 까맣게 잊고 있다가, 자그마한 수첩이 아래 봉투에 넣어져 도착했습니다.
사용자 삽입 이미지

우편 봉투


수첩은 전체적으로 회색을 띠고 있었습니다.
사용자 삽입 이미지

pocket diary for physicists

2007~2008 용인데 날짜가 딱 9월 3일 월요일부터 시작해서, 이번 가을학기부터 사용하면 될 듯 합니다.
다음은 한국 부분이 있어서 찍어본 사진입니다. 국내 물리학과가 있는 대학들이 소개되어 있었습니다.
HEP라는 건 High Energy Physics_고에너지물리라는 뜻 같네요.
사용자 삽입 이미지

Republic of Korea in the diary


반응형

+ Recent posts

티스토리툴바