'레비-시비타' 태그의 글 목록

레비-시비타

Mathematical Physics 2 2007.09.06

Mathematical Physics 2

세레 2007. 9. 6. 22:37

2007. 9. 6. 22:37

Recapitulation

- Vector space V (to axioms)

- basis

- inner product $<\vec{v},\vec{u}>$

- dot product VV->k

-cross product VV->V

$\vec{B} \times \vec{C} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ B_{x} & B_{y} & B_{z} \\ C_{x} & C_{y} & C_{z} \end{vmatrix} = \left | \vec{B} \right \vert \left | \vec{C} \right \vert \sin \theta_{k} \hat{n}$

$dt \begin{pmatrix} a & b \\ c & d \end{pmatrix} =ad-bc$
$dt \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} =aei+dhc+bfy-(ceg+bdi+hfa)$

diagonal하게 생각하면, 기억하기 쉽다.

geometrical meaning of $\vec{B} \times \vec{C}$

벡터 B가 x축 위에 누워있고, 벡터 C가 xy평면의 1사분면 중 어느 점을 가리키고 있는 상황이다.
벡터 B와 벡터 C 사이의 각은 $θ B C$ 이다.

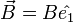
$\vec{B}=B \hat{e_{1}}$ $\vec{C}=C \cos \theta_{BC} \hat{e_{1}} + C \sin \theta_{BC} \hat{e_{2}}$ $\Rightarrow \vec{B} \times \vec{C} = BC \cos \theta_{BC} \hat{e_{1}} \times \hat{e_{1}} + BC \sin \theta_{BC} \hat{e_{1}} \times \hat{e_{2}}$ $=BC \sin \theta_{BC} \hat{e_{3}}$

$\hat{e_{1}} \times \hat{e_{1}} = \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{vmatrix} =0$

$\hat{e_{1}} \times \hat{e_{2}} = \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} = \hat{e_{3}}$

$\hat{e_{1}} \times \hat{e_{2}} = \hat{e_{3}}; \hat{e_{2}} \times \hat{e_{3}} = -\hat{e_{1}}; \hat{e_{3}} \times \hat{e_{1}} = \hat{e_{2}}$ $\hat{e_{2}} \times \hat{e_{1}} = -\hat{e_{3}}; \hat{e_{3}} \times \hat{e_{2}} = -\hat{e_{1}}; \hat{e_{3}} \times \hat{e_{1}} = -\hat{e_{2}}$

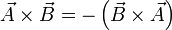
$\vec{A} \times \vec{B} = - \left( \vec{B} \times \vec{A} \right)$

순서를 바꾸면 negation이 되는 이유

$\begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix}$ $\begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{vmatrix}$

triple scalar product

$\vec{A} \cdot \left( \vec{B} \times \vec{C} \right)$

$\left | \vec{A} \right \vert \underbrace{\left | \vec{B} \right \vert \left | \vec{C} \right \vert \sin \theta_{BC}}_{area} \cos \beta$

geometrical meaning: volume of pipe

triple cross product

$\vec{A} \times \left( \vec{B} \times \vec{C} \right) \ne \left( \vec{A} \times \vec{B} \right) \times \vec{C}$ VVV->V $\vec{A} \times \left( \vec{B} \times \vec{C} \right) = -\vec{C} \times \left( \vec{A} \times \vec{B} \right) = \vec{C} \times \left( \vec{B} \times \vec{A} \right)$ $\vec{A} \times \left( \vec{B} \times \vec{C} \right) = \vec{B} \left( \vec{A} \cdot \vec{C} \right) -\vec{C} \left( \vec{A} - \vec{B} \right)$

Levi-civita symbol

ε i j k

http://en.wikipedia.org/wiki/Levi-Civita_symbol

$ε 123 = ε 231 = ε 312 = 1$ $ε 132 = ε 213 = ε 321 = - 1$

나란히 있는 두 숫자의 순서가 바뀌면 1의 부호가 바뀐다라고 생각하면 쉬움. 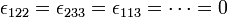$\epsilon_{122}=\epsilon_{233}=\epsilon_{113}= \cdots =0$

같은 숫자가 두개 있으면 0이라고 생각하기.

& Any permutations of two indices will introduce "-" sign

Usefulness of $ε i j k$

$\hat{e_{i}} \times \hat{e_{j}} = \sum_{k} \epsilon_{ijk} \hat{e_{k}}$ where i,j,k=1,2,3

eg.

$\hat{e_{1}} \times \hat{e_{2}} = \sum_{k} \epsilon_{12k}\hat{e_{k}}=\underbrace{\epsilon_{123}}_{1}$

Another useful symbol: Kronedeker delta

http://en.wikipedia.org/wiki/Kronecker_delta

http://mathworld.wolfram.com/KroneckerDelta.html

$\delta_{ij} = \begin{cases} 0, & \mbox{if }i \ne j \\ 1, & \mbox{if }i=j \end{cases}$

eg. (m & n are dummy indices)

$\vec{B} \times \vec{C} = \left( \sum_{m=1}^{3} B_{m} \hat{e_{m}} \right) \times \left( \sum_{n=1}^{3} C_{n} \hat{e_{n}} \right)$

$= \sum_{m, n} B_{m}C_{n} \underbrace{\left( \hat{e_{m}} \times \hat{e_{n}} \right)}_{\sum_{j} \epsilon_{mnj} \hat{e_{j}}}$

$=\sum_{m,n,j} B_{m}C_{n} \epsilon_{mnj} \hat{e_{j}}$

jth component

∑	B_mC_nε_mnj
m,n

∑	B_mC_nε_mn1
m,n

$= B 2 C 3 - B 3 C 2$

$\sum_{k=1}^{3} \epsilon_{mnk} \epsilon_{ijk} = \delta_{mi} \delta_{nj} - \delta_{mj} \delta_{ni}$

∑	ε_mjkε_njk = 2δ_mn
j,k

$\sum_{i,j,k} \epsilon_{ijk}^{2}=6$

eg 2. (Einstein convention - sum을 나타내는 sigma 기호 생략)

$\vec{A} \times \left( \vec{B} \times \vec{C} \right)$

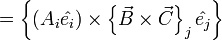
$= \left \{ \left( A_{i} \hat{e_{i}} \right) \times \left \{ \vec{B} \times \vec{C} \right \}_{j} \hat{e_{j}} \right \}$

$= A_{i} \underbrace{\left( \vec{B} \times \vec{C} \right)_{j}}_{B_{m}C_{n} \epsilon_{mnj}} \underbrace{\hat{e_{i}} \times \hat{e_{j}}}_{\sum_{k} \underbrace{\epsilon_{ijk}}_{-\epsilon_{ikj}} \hat{e_{k}}}$

$=-A_{i}B_{m}C_{n} \underbrace{\epsilon_{mnj} \epsilon_{ikj}}_{\delta_{mi} \delta_{nk} - \delta_{mk} \delta_{ni}} \hat{e_{k}}$

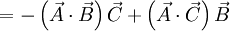
$=-A_{i}B_{m}C_{n} \delta_{mi} \delta_{nk} \hat{e_{k}} + A_{i}B_{m}C_{n} \delta_{mk} \delta_{ni} \hat{e_{k}}$ $=-A_{m}B_{m}C_{n} \delta_{nk} \hat{e_{k}} + A_{i}B_{k}C_{n} \delta_{ni} \hat{e_{k}}$ $=-A_{m}B_{m}C_{n} \hat{e_{n}} + A_{n}B_{k}C_{n} \hat{e_{k}}$ $=-\left( \vec{A} \cdot \vec{B} \right) \vec{C} + \left( \vec{A} \cdot \vec{C} \right) \vec{B}$