물리
- 파인만의 과학이란 무엇인가 2010.06.03
- 볼츠만의 원자 2010.05.27
- 초끈이론의 진실 2010.05.24
- 광전 효과 2010.05.01
- Mathematical Physics 2 2007.09.06
- Mathematical Physics 1 2007.09.03
- Gravitation and Central Forces 1 2007.09.03
- 물리학자를 위한 휴대용 (연간 예정) 수첩 2007.09.01
- 이휘소 평전을 읽었습니다. 2007.08.03
파인만의 과학이란 무엇인가
볼츠만의 원자
볼츠만은 헬름홀츠와 맥스웰과도 교류했는데, 비사교적인 인물이라서 그런지 의견을 표현할 때도 직설적이고 후에는 자신의 가족과 고립하여 연구에 몰두했던 것으로 나와 있다. 볼츠만이 결혼하고 가족을 이루는 모습에서, 그의 개인적인 인생은 어떠했는지 알 수 있었다. 열역학에서 H라는 기호가 E를 잘못 읽은 데에서 비롯한 뒷 이야기가 신기했다.
엔트로피는 정보 이론의 아버지 클라우드 섀넌에 의해 정보를 측정하는 양으로 새롭게 해석되어서, 블랙홀과 엔트로피를 연관지은 베켄슈타인-호킹 엔트로피에 의하면 어떤 정보를 담을 수 있는 한계는 부피가 아니라 면적에 비례한다는 재미있는 이론들이 많다. 관심 있게 통계 물리를 공부하던 때에, 배우는 방향과 부합하는 책이라서 더 유익했다.
|
|||||||||||
초끈이론의 진실
광전 효과
여기서
참고 자료 (Following Creative Commons Attribution, ShareAlike license)
http://en.wikipedia.org/wiki/Photoelectric_effect
http://en.wikipedia.org/wiki/Albert_Einstein
http://en.wikipedia.org/wiki/Light
http://en.wikipedia.org/wiki/Planck_constant
http://en.wikipedia.org/wiki/Electromagnetic_field
http://en.wikipedia.org/wiki/Black_body
Mathematical Physics 2
Recapitulation
- Vector space V (to axioms)
- basis
- inner product 
- dot product VV->k
-cross product VV->V



diagonal하게 생각하면, 기억하기 쉽다.
geometrical meaning of 
벡터 B가 x축 위에 누워있고, 벡터 C가 xy평면의 1사분면 중 어느 점을 가리키고 있는 상황이다.
벡터 B와 벡터 C 사이의 각은 θBC이다.
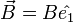







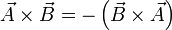
순서를 바꾸면 negation이 되는 이유


triple scalar product


geometrical meaning: volume of pipe
triple cross product
 VVV->V
VVV->V 

Levi-civita symbol
εijkhttp://en.wikipedia.org/wiki/Levi-Civita_symbol
ε123 = ε231 = ε312 = 1 ε132 = ε213 = ε321 = − 1
나란히 있는 두 숫자의 순서가 바뀌면 1의 부호가 바뀐다라고 생각하면 쉬움. 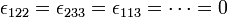
같은 숫자가 두개 있으면 0이라고 생각하기.
& Any permutations of two indices will introduce "-" sign
Usefulness of εijk
 where i,j,k=1,2,3
where i,j,k=1,2,3
eg.

Another useful symbol: Kronedeker delta
http://en.wikipedia.org/wiki/Kronecker_delta
http://mathworld.wolfram.com/KroneckerDelta.html

eg. (m & n are dummy indices)



jth component
| ∑ | BmCnεmnj |
| m,n |
| ∑ | BmCnεmn1 |
| m,n |
= B2C3 − B3C2

| ∑ | εmjkεnjk = 2δmn |
| j,k |

eg 2. (Einstein convention - sum을 나타내는 sigma 기호 생략)

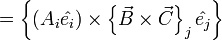





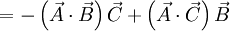
gradient operator


 -(1)
-(1)
여기서 
식 (1)이 최대가 되려면  에서 maximum at θ = 0
에서 maximum at θ = 0
θ는  벡터와
벡터와  벡터 사이의 각
벡터 사이의 각
Mathematical Physics 1
Q: What is a vector?
short answer: physical quantities that have a magnitude as well as a direction.
eg.
r, v, a in vector
exteded definition (answer): an element of a vector space.
Q: What is a vector space?
answer: a set whose elements are vectors that obey a certain set of rules.
1. If
2. If
3.
4.
5.
6.
7.
8.
9.
10.
eg 0.
eg 1.
cf.
eg 2. V:

eg 3. Laplace equation (→ normal modes)
<basis> a set of linearly independent vectors that spans V. say
<inner product>
a mapping that maps two vectors to a scalar. < vi,vj >1) < au1 + bu2,v > = a < u1,v > + b < u2,v > (a,b are constants)
2)
3)
eg 1. dot product
eg 2.

Dot product
Cross product

Gravitation and Central Forces 1
지구에서 관측되는 별의 움직임이 서에서 동으로 갈 때 거꾸로 움직여서, 고리를 그리는 현상이 발견됨.
Ptolemy: epicycle(주전원, 그 중심이 다른 큰 원의 툴레 위를 회전하는 작은 원)을 주장.
코페르니쿠스: 지동설 주장.
Johannes Kepler: Tycho Brahe의 데이터를 갖고 세 법칙을 발견함.
1. 타원궤도
2. 면적속도 일정
3. 주기 T의 제곱은 장축의 세제곱에 비례
갈릴레오 갈릴레이:
Isaac Newton: Universal gravitation(만유인력)
Newton의 3개 운동법칙 - 관성, F=ma, 작용-반작용

formula of universal gravitation
F의 앞 첨자는 힘을 경험하는 곳, 뒤 첨자는 힘의 source이다.
위에서 r 벡터는 i에서 j로 향하는 위치벡터.
만유인력 상수
gravitational constant
물리학자를 위한 휴대용 (연간 예정) 수첩

우편 봉투
수첩은 전체적으로 회색을 띠고 있었습니다.

pocket diary for physicists
다음은 한국 부분이 있어서 찍어본 사진입니다. 국내 물리학과가 있는 대학들이 소개되어 있었습니다.
HEP라는 건 High Energy Physics_고에너지물리라는 뜻 같네요.

Republic of Korea in the diary
이휘소 평전을 읽었습니다.
이휘소라는 분에 대해 가장 사실적으로 저술했다고 알려진 "이휘소 평전"이라는 책을 빌려 읽었습니다. 목표에 대한 실천력과 집중력이 대단하신 분이라고 생각합니다. 만일 그 때 불운의 사고가 일어나지 않았다면 대한민국이 국제 사회에서 차지하는 과학에 대한 비중이 어떻게 바뀌었을지 상상이 안 됩니다. 물리학도를 꿈꾸는 많은 사람들과, 이휘소라는 분을 소설로만 접해보신 분에게 좋은 도서라고 생각합니다.
