반응형
플랑크 상수를 이용해서 여러가지 계산을 해볼 수 있습니다. 빛의 속도를 c라고 하고 그 값은 3 \times 10^{8} \rm ~ m/s라고 가정합시다. (진공에서의 빛의 속도는 오차 없이 정확히 299,792,458 m/s입니다. 왜냐하면 SI 단위인 미터의 단위가 빛이 1/(299 792 458) 초만큼 가는 거리로 정의되었기 때문이죠.) 이제 hc 값을 계산해 봅시다.

h = 6.626 \times 10^{-34} ~ \rm J \cdot s
hc = (6.626 \times 10^{-34} ~ \rm J \cdot s )(3 \times 10^{8} \rm ~ m/s)
= 6.626 \times 3 \times 10^{-26} \rm ~ J \cdot m
1 \rm ~ eV = 1.6 \times 10^{-19} ~ J
따라서 1 \rm ~ J = \frac{1}{1.6} \times 10^{19} \rm ~ eV
hc = 6.626 \times 3 \times 10^{-26} \times \frac{1}{1.6} \times 10^{19} \rm ~ eV \cdot m
= \left( \frac{6.626 \times 3}{1.6} \right) 10^{-7} \rm ~ eV \cdot m
그런데, 1 \rm ~ eV = 10^{-6} ~ MeV 이고, 1 \rm ~ fm = 10^{-15} ~ m임을 이용하면
hc = 1242.375 \rm ~ MeV \cdot m \approx 1240 ~ \rm MeV \cdot fm이 됩니다.

위 수식들을 자세히 살펴보시면 h나 c는 이탤릭체로 표현되어 있는데 단어는 전부 로마자(정자) 형태를 하고 있음을 보실 수 있습니다. 과학적 논의를 위한 수식을 쓸 때에는 물리적 상수나 수학 상수처럼 값이 고정되어 변하지 않는 값이지만 그 값을 대신하여 쓰는 경우에는 이탤릭체로 표현을 합니다. 그리고 매개변수나 독립변수 들도 이탤릭체로 표현되는데 이렇게 이탤릭체를 많이 쓰기 때문에 TeX에서 기본 서체를 이탤릭으로 정한 것 같습니다.

하지만 SI 7개 단위를 비롯한 각종 CGS 단위, SI 접두사 등은 변수나 상수가 아니므로, 숫자 값에서 구분하기 위해 로마자로 띄어 써서 표시해야 합니다. 이를 TeX에서 표현하려면 \rm을 앞에 붙여 기본 이탤릭 설정으로 로마자 형식으로 바꾸고 ~으로 띄어 써야 합니다. (아래아 한글 프로그램의 수식에서는 TeX 문법과 조금 다르게 필요한 수식을 다 입력하시고 그냥 rm을 입력하고 키보드 1옆에 있는 `으로 띄어 쓰기를 합니다. 그냥 수식이 없는 상태에서 `을 누르면 TeX의 \cdot 처럼 가운뎃점으로 표시해주더군요.) 이에 관련된 PDF 문서로는 Mills, I. M.; Metanomski, W. V. (December 1999), On the use of italic and roman fonts for symbols in scientific text, IUPAC Interdivisional Committee on Nomenclature and Symbols을, 관련된 웹 페이지로는 SI writing style (Wikipedia)을 참조하시면 됩니다.
 
참고자료 License: http://creativecommons.org/licenses/by-sa/3.0/
http://en.wikipedia.org/wiki/Planck_constant
http://en.wikipedia.org/wiki/Italic_type
http://en.wikipedia.org/wiki/Speed_of_light
반응형
반응형
플랑크상수는 물리상수 중에 하나로, 광자의 에너지를 표현할 때나, 드브로이의 파장 식, 슈뢰딩거 방정식 등 많은 물리 수식에 등장하곤 합니다. 또한, 양자역학에서 양자의 크기를 기술하기 위해 사용됩니다.
영문 위키피디아에 의하면 플랑크 상수는 다음과 같습니다. 거시적인 계산의 경우 줄 단위를, 미시적인 계산일 경우 eV를 선택해서 사용하는 것이 계산에 편리합니다.
Values of h     Units
6.62606896(33)×10^−34     J·s
4.13566733(10)×10^−15     eV·s
6.62606896(33)×10^−27     erg·s
Values of ħ     Units
1.054571628(53)×10^−34     J·s
6.58211899(16)×10^−16     eV·s
1.054571628(53)×10^−27     erg·s
위 값중 많이 쓰는 줄 단위와 eV 단위의 플랑크상수를 소수 점 넷째자리에서 반올림하면 다음과 같습니다. 그냥 플랑크 상수 값 h는 h = 6.626 \times 10^{-34}\rm ~ J \cdot s = 4.136 \times 10^{-15} \rm ~ eV \cdot s입니다. 그리고 플랑크 상수에 2 \pi를 나눈 h bar (에이치 바, 하바)값은 \hbar = 1.055 \times 10^{-34} \rm ~ J \cdot s = 6.582 \times 10^{-16} \rm ~ eV \cdot s이 됩니다. 두 값 모두 물리적으로 중요한 의미를 갖는 상수이고, 물리 수식에서 자주 등장하므로 두 단위로 외워두면 계산에 편리합니다.



참고자료 License: http://creativecommons.org/licenses/by-sa/3.0/
http://en.wikipedia.org/wiki/Planck_constant
반응형
반응형
빛의 파동성의 증거에도, 알베르트 아인슈타인은 1905년 그의 유명한 논문 중 광전효과에 대한 현상을 양자들로 구성된 전자기장이라고 처음으로 제안하였다. 여기서 양자들이란 에너지의 묶음으로 현재 와서는 광자라고 불린다. 아인슈타인은 물리학자 막스 플랑크가 공동 복사(Cavity radiation)를 분석한 결과에 영향을 받아 광자가 다음과 같은 에너지를 갖고 있다고 제안했다.

E = h \nu
여기서 \nu는 빛의 주파수이고 상수 h는 기초 상수인 플랑크 상수이다. 그 값은 6.63 \times 10^{-34} \rm~J \cdot s이다. 광전효과에서 광자는 깨끗한 금속 표면에 충돌한다. 금속에서는 전자가 분출된다. 이 전자는 광전자라고 한다.

참고 자료 (Following Creative Commons Attribution, ShareAlike license)

http://en.wikipedia.org/wiki/Photoelectric_effect
http://en.wikipedia.org/wiki/Albert_Einstein
http://en.wikipedia.org/wiki/Light
http://en.wikipedia.org/wiki/Planck_constant
http://en.wikipedia.org/wiki/Electromagnetic_field
http://en.wikipedia.org/wiki/Black_body
반응형
반응형
23쪽
피터가 말했습니다. 가장 가까이 있는 책을 집으세요. 23쪽을 펴세요. 다섯 번째 문장을 찾으세요. 이 지시사항들과 함께, 그 문장을 당신의 블로그에 올리세요.

The axix of this rotation is perpendicular to the force F, and it is also perpendicular to the line OP; therefore, the direction of the torque vector N is along the axis of rotation.

피터는 과학자.
반응형
저작자표시 비영리 동일조건

반응형

Recapitulation

- Vector space V (to axioms)

- basis

- inner product <\vec{v},\vec{u}>

- dot product VV->k

-cross product VV->V

\vec{B} \times \vec{C} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}\\ B_{x} & B_{y} & B_{z} \\ C_{x} & C_{y} & C_{z} \end{vmatrix} = \left | \vec{B} \right \vert \left | \vec{C} \right \vert \sin \theta_{k} \hat{n}

 dt \begin{pmatrix} a & b \\ c & d \end{pmatrix} =ad-bc
dt \begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} =aei+dhc+bfy-(ceg+bdi+hfa)

diagonal하게 생각하면, 기억하기 쉽다.

geometrical meaning of \vec{B} \times \vec{C}

벡터 B가 x축 위에 누워있고, 벡터 C가 xy평면의 1사분면 중 어느 점을 가리키고 있는 상황이다.
벡터 B와 벡터 C 사이의 각은 θBC이다.

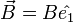
\vec{B}=B \hat{e_{1}} \vec{C}=C \cos \theta_{BC} \hat{e_{1}} + C \sin \theta_{BC} \hat{e_{2}} \Rightarrow \vec{B} \times \vec{C} = BC \cos \theta_{BC} \hat{e_{1}} \times \hat{e_{1}} + BC \sin \theta_{BC} \hat{e_{1}} \times \hat{e_{2}} =BC \sin \theta_{BC} \hat{e_{3}}

 \hat{e_{1}} \times \hat{e_{1}} = \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 1 & 0 & 0 \end{vmatrix} =0

\hat{e_{1}} \times \hat{e_{2}} = \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} = \hat{e_{3}}

\hat{e_{1}} \times \hat{e_{2}} = \hat{e_{3}}; \hat{e_{2}} \times \hat{e_{3}} = -\hat{e_{1}}; \hat{e_{3}} \times \hat{e_{1}} = \hat{e_{2}} \hat{e_{2}} \times \hat{e_{1}} = -\hat{e_{3}}; \hat{e_{3}} \times \hat{e_{2}} = -\hat{e_{1}}; \hat{e_{3}} \times \hat{e_{1}} = -\hat{e_{2}}

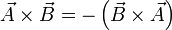
\vec{A} \times \vec{B} = - \left( \vec{B} \times \vec{A} \right) 

순서를 바꾸면 negation이 되는 이유

\begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{vmatrix} \begin{vmatrix} \hat{e_{1}} & \hat{e_{2}} & \hat{e_{3}} \\ 0 & 1 & 0 \\ 1 & 0 & 0 \end{vmatrix}


triple scalar product

\vec{A} \cdot \left( \vec{B} \times \vec{C} \right)

\left | \vec{A} \right \vert \underbrace{\left | \vec{B} \right \vert \left | \vec{C} \right \vert \sin \theta_{BC}}_{area} \cos \beta

geometrical meaning: volume of pipe


triple cross product

\vec{A} \times \left( \vec{B} \times \vec{C} \right) \ne \left( \vec{A} \times \vec{B} \right) \times \vec{C} VVV->V \vec{A} \times \left( \vec{B} \times \vec{C} \right) = -\vec{C} \times \left( \vec{A} \times \vec{B} \right) = \vec{C} \times \left( \vec{B} \times \vec{A} \right) \vec{A} \times \left( \vec{B} \times \vec{C} \right) = \vec{B} \left( \vec{A} \cdot \vec{C} \right) -\vec{C} \left( \vec{A} - \vec{B} \right)

Levi-civita symbol

εijk

http://en.wikipedia.org/wiki/Levi-Civita_symbol

ε123 = ε231 = ε312 = 1 ε132 = ε213 = ε321 = − 1

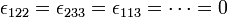
나란히 있는 두 숫자의 순서가 바뀌면 1의 부호가 바뀐다라고 생각하면 쉬움. \epsilon_{122}=\epsilon_{233}=\epsilon_{113}= \cdots =0

같은 숫자가 두개 있으면 0이라고 생각하기.

& Any permutations of two indices will introduce "-" sign


Usefulness of εijk

\hat{e_{i}} \times \hat{e_{j}} = \sum_{k} \epsilon_{ijk} \hat{e_{k}} where i,j,k=1,2,3

eg.

\hat{e_{1}} \times \hat{e_{2}} = \sum_{k} \epsilon_{12k}\hat{e_{k}}=\underbrace{\epsilon_{123}}_{1}

Another useful symbol: Kronedeker delta


http://en.wikipedia.org/wiki/Kronecker_delta

http://mathworld.wolfram.com/KroneckerDelta.html

\delta_{ij} = \begin{cases} 0, & \mbox{if }i \ne j \\ 1, & \mbox{if }i=j \end{cases}

eg. (m & n are dummy indices)

\vec{B} \times \vec{C} = \left( \sum_{m=1}^{3} B_{m} \hat{e_{m}} \right) \times \left( \sum_{n=1}^{3} C_{n} \hat{e_{n}} \right)

 = \sum_{m, n} B_{m}C_{n} \underbrace{\left( \hat{e_{m}} \times \hat{e_{n}} \right)}_{\sum_{j} \epsilon_{mnj} \hat{e_{j}}}

=\sum_{m,n,j} B_{m}C_{n} \epsilon_{mnj} \hat{e_{j}}

jth component

∑ BmCnεmnj
m,n
∑ BmCnεmn1
m,n

= B2C3 − B3C2

\sum_{k=1}^{3} \epsilon_{mnk} \epsilon_{ijk} = \delta_{mi} \delta_{nj} - \delta_{mj} \delta_{ni}

∑ εmjkεnjk = 2δmn
j,k

\sum_{i,j,k} \epsilon_{ijk}^{2}=6


eg 2. (Einstein convention - sum을 나타내는 sigma 기호 생략)

\vec{A} \times \left( \vec{B} \times \vec{C} \right)

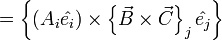
 = \left \{ \left( A_{i} \hat{e_{i}} \right) \times \left \{ \vec{B} \times \vec{C} \right \}_{j} \hat{e_{j}} \right \}

= A_{i} \underbrace{\left( \vec{B} \times \vec{C} \right)_{j}}_{B_{m}C_{n} \epsilon_{mnj}} \underbrace{\hat{e_{i}} \times \hat{e_{j}}}_{\sum_{k} \underbrace{\epsilon_{ijk}}_{-\epsilon_{ikj}} \hat{e_{k}}}

 =-A_{i}B_{m}C_{n} \underbrace{\epsilon_{mnj} \epsilon_{ikj}}_{\delta_{mi} \delta_{nk} - \delta_{mk} \delta_{ni}} \hat{e_{k}} 

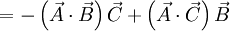
=-A_{i}B_{m}C_{n} \delta_{mi} \delta_{nk} \hat{e_{k}} + A_{i}B_{m}C_{n} \delta_{mk} \delta_{ni} \hat{e_{k}} =-A_{m}B_{m}C_{n} \delta_{nk} \hat{e_{k}} + A_{i}B_{k}C_{n} \delta_{ni} \hat{e_{k}} =-A_{m}B_{m}C_{n} \hat{e_{n}} + A_{n}B_{k}C_{n} \hat{e_{k}} =-\left( \vec{A} \cdot \vec{B} \right) \vec{C} + \left( \vec{A} \cdot \vec{C} \right) \vec{B}


gradient operator

\nabla \phi \left( x,y \right)

=\frac{\partial \phi}{\partial x} \hat{e_{x}} + \frac{\partial \phi}{\partial y} \hat{e_{y}}

d \phi \left( x,y \right) = \frac{\partial \phi}{\partial x} dx + \frac{\partial \phi}{\partial y} dy = \nabla \phi \cdot d \vec{r} -(1)

여기서 d \vec{r} = dx \hat{e_{x}} + dy \hat{e_{y}}

식 (1)이 최대가 되려면 \cos \theta \left | \nabla \phi \right \vert \left | d \vec{r} \right \vert 에서 maximum at θ = 0

θ는 d \vec{r} 벡터와 \nabla \phi 벡터 사이의 각

반응형
반응형

Q: What is a vector?



short answer: physical quantities that have a magnitude as well as a direction.
eg.
사용자 삽입 이미지

r, v, a in vector


exteded definition (answer): an element of a vector space.

Q: What is a vector space?


answer: a set whose elements are vectors that obey a certain set of rules.
1. If ,
2. If , then (c: constant)
3.
4. such that
5. such that
6.
7.
8.
9.
10.
eg 0.
eg 1.
cf.

eg 2. V: matrices

eg 3. Laplace equation (→ normal modes)

<basis> a set of linearly independent vectors that spans V. say
forms a basis for V


if and only if ai = 0
and (any vectors in V)

<inner product>

a mapping that maps two vectors to a scalar. < vi,vj >
1) < au1 + bu2,v > = a < u1,v > + b < u2,v > (a,b are constants)
2)
3) or 0 if and only if
eg 1. dot product



eg 2.


Dot product






Cross product



반응형
반응형
6. Gravitation and Central Forces (중력과 중심력)
지구에서 관측되는 별의 움직임이 서에서 동으로 갈 때 거꾸로 움직여서, 고리를 그리는 현상이 발견됨.
Ptolemy: epicycle(주전원, 그 중심이 다른 큰 원의 툴레 위를 회전하는 작은 원)을 주장.
코페르니쿠스: 지동설 주장.
Johannes Kepler: Tycho Brahe의 데이터를 갖고 세 법칙을 발견함.
1. 타원궤도
2. 면적속도 일정
3. 주기 T의 제곱은 장축의 세제곱에 비례
갈릴레오 갈릴레이:
Isaac Newton: Universal gravitation(만유인력)
Newton의 3개 운동법칙 - 관성, F=ma, 작용-반작용
사용자 삽입 이미지

formula of universal gravitation


F의 앞 첨자는 힘을 경험하는 곳, 뒤 첨자는 힘의 source이다.
위에서 r 벡터는 i에서 j로 향하는 위치벡터.
만유인력 상수
사용자 삽입 이미지

gravitational constant


반응형
반응형
PDG에서 온 소포 이후 까맣게 잊고 있다가, 자그마한 수첩이 아래 봉투에 넣어져 도착했습니다.
사용자 삽입 이미지

우편 봉투


수첩은 전체적으로 회색을 띠고 있었습니다.
사용자 삽입 이미지

pocket diary for physicists

2007~2008 용인데 날짜가 딱 9월 3일 월요일부터 시작해서, 이번 가을학기부터 사용하면 될 듯 합니다.
다음은 한국 부분이 있어서 찍어본 사진입니다. 국내 물리학과가 있는 대학들이 소개되어 있었습니다.
HEP라는 건 High Energy Physics_고에너지물리라는 뜻 같네요.
사용자 삽입 이미지

Republic of Korea in the diary


반응형
반응형
http://hardware.slashdot.org/article.pl?sid=07/08/14/0023202&from=rss

Rensselaer Polytechnic Institute의 연구원이 탄소나노튜브(Carbon nanotube [Wikipedia])와 전해질을 종이 기판에 주입함으로써 조합 건전지/축전지를 개발했다고 밝혔습니다. 납, 카드뮴, 수은 등으로 많은 전지들이 만들어지고 있는데, 이런 친환경적 기술에 많은 관심이 필요하다고 생각해요. 이 물질은 접을 수 있고, 돌돌 말 수도 있고, 원하는 형태로 뜰 수도 있다고 해요. 아직 대량으로 장치를 제조하는 방법이 개발되지는 않았지만, 신문용지처럼 롤러 사이에 인쇄하는 형태를 마음에 두고 있다고 하네요. (어쩌면 인쇄하는 형태라고 봐도 되겠네요.)

위에서 탄소나노튜브란 말이 나온 김에 다른 이야기를 해 봅니다. 탄소나노튜브는 풀러렌(Fullerene [Wikipedia], C60)이라는 축구공 모양의 탄소화합물에서 파생되었습니다. 신기한 특성에서 몇 가지를 꼽하보자면 일단 튼튼하고, 전기를 통한다는 점이에요. 현재 우주에 가려면, 우주선을 발사시켜서 가야 하는데, 다른 방법으로는 우주 엘리베이터(Carbon nanotube, space elevator [Wikipedia])를 만드는 것이죠. 우주로 가는 엘리베이터를 만들려면 가볍고 튼튼한 소재가 필요하죠. 그런데 금속성 물질로 만든다면, 밀도가 높아서 하중을 어떻게 견디게 하느냐가 이슈가 되는데요. 비록 현재 기술에서 많은 발전이 필요하지만, 탄소나노튜브가 우주 엘리베이터의 소재로 검토되고 있다고 합니다. 개발만 된다면, 우주로 가는 길은 훨씬 간편해지겠죠. 개인적으로"은하철도 999"의 우주철도도 공상적 요소가 강하지만 아주 불가능하지는 않을 것 같아요. (제가 바라고 있기도 하지만 그만큼 기술 발전이 필요한 시간을 생각해보면, 아쉽게도 저는 보기 힘들 것 같네요.)

글에 오류가 있다면, 지적은 언제든 환영입니다. :-)
반응형

+ Recent posts

티스토리툴바